| Inequações exponenciais | |||||||||||||||||||||||||||||||||||
| Inequações exponenciais | |||||||||||||||||||||||||||||||||||
As inequações que envolvem funções exponenciais são consideradas inequações
exponenciais. Veja os exemplos:
Na resolução das inequações exponenciais analisamos os casos nos quias:
a > 1
Quando função f(x) = ax apresenta base maior que 1, (a > 1), desprezamos as bases comuns e mantemos o sinal da desigualdade em relação aos expoentes.
Exemplos:
Para determinar o conjunto verdade da inequação 8x ≤ 64, sendo U = R, inicialmente tornamos as bases iguais:
Para determinar o conjunto verdade da inequação 8x ≤ 64, sendo U = R, inicialmente tornamos as bases iguais:
8x ≤ 64 ⇒ 23x ≤ 26
Como a base 2 é maior que 1, mantemos o sinal da desigualdade em relação aos expoentes.
| 23x ≤ 26 ⇒ 3x ≤ 6 ⇒ | x ≤ | 6 | x ≤ 2 | V = { x ∈ R| x ≤ 2 } | |||||||||||||||||||||||
| 3 | |||||||||||||||||||||||||||
o < a < 1
Quando a função f(x) = ax apresenta base maior que zero e menor que 1 ( 0 < a < 1 ), desprezando as base comuns e invertemos o sinal da desigualdade em relação aos expoentes.
Exemplo:
| Para determinar o conjunto verdade da inequação |  |
, sendo U = R, observe | ||||||||||||||||||||||||||||||||
| que, como a base | 1 | é maior que 0 e menor que 1 , invertemos o sinal da desigualdade em | ||||||||||||||||||||||||||||||||
| 3 | ||||||||||||||||||||||||||||||||||
| relação aos expoentes. | ||||||||||||||||||||||||||||||||||
V = { X ∈ R | x < 2 }


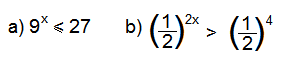



Nenhum comentário:
Postar um comentário